Mesh support in escher

0x1 总体介绍

Graphics中各种图形的渲染是通过许多小的三角形的渲染拼接组成的，Mesh的过程是把需要渲染的图形划分成许多小三角形的过程.
Escher中的mesh过程需要把Rectangle, Circle, Ring, Sphere等形状的显示对象划分成小三角形，然后把小三角形的数据通过Vulkan API来驱动GPU显示.

下图是escher中mesh相关类的类图

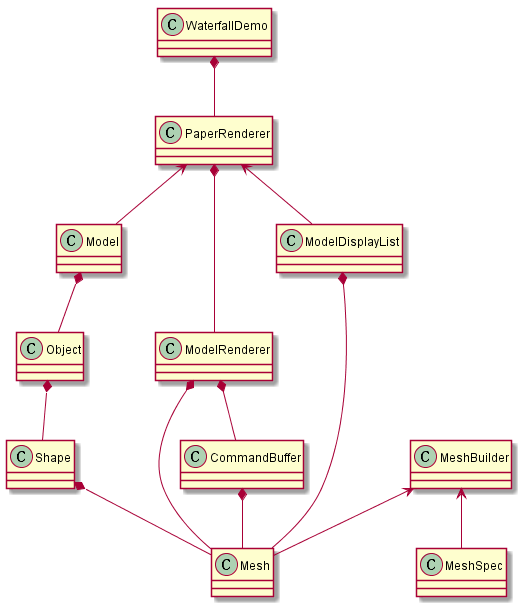
下面简单介绍一下这些类

Mesh创建过程中，
MeshBuilder根据MeshSpec的设置生成对应的Mesh.
Mesh的vertex/index数据保存到CommandBuffer中，

Mesh渲染过程中，
对应的PageRenderer生成对应的Object，每一个Object都有对应的Mesh，这些Object挂接到Model下面.
然后根据Model中包含的Mesh生成ModelDisplayList，然后遍历这个ModelDisplayList，把Mesh中的vertex/index数据传入CommandBuffer中，从而让GPU渲染的时候能够访问到这些数据.

0x2 各种shape的mesh过程

0x21 MeshBuilder介绍

MeshBuilder提供接口把vertex data和index data保存起来.

其中保存的数据结构如下,
vertex_stagingbuffer保存vertex数据，index_stagingbuffer保存index数据.
vertex_stagingbuffer和index_stagingbuffer的内存空间是通过GpuUploader::Writer来分配的.

const size_t max_vertex_count_;
const size_t max_index_count_;
const size_t vertex_stride_;
uint8_t* vertex_staging_buffer_;
uint32_t* index_staging_buffer_;
size_t vertex_count_ = 0;
size_t index_count_ = 0;

下面是其提供设置vertex data和index data的接口.
注意下面的接口都返回 *this， 这是为了链式表达式的需要.

inline MeshBuilder& MeshBuilder::AddIndex(uint32_t index) {
  FXL_DCHECK(index_count_ < max_index_count_);
  index_staging_buffer_[index_count_++] = index;
  return *this;
}

inline MeshBuilder& MeshBuilder::AddVertexData(const void* ptr, size_t size) {
  FXL_DCHECK(vertex_count_ < max_vertex_count_);
  FXL_DCHECK(size <= vertex_stride_);
  size_t offset = vertex_stride_ * vertex_count_++;
  memcpy(vertex_staging_buffer_ + offset, ptr, size);
  return *this;
}

template <typename VertexT>
MeshBuilder& MeshBuilder::AddVertex(const VertexT& v) {
  AddVertexData(&v, sizeof(VertexT));
  return *this;
}

然后调用Build()接口生成mesh对象.

0x22 SimpleRectangle

下面是生成SimpleRectangle的mesh的代码，SimpleRectangle是普通的非圆角Rectangle.
从这个代码中可以看到，该mesh过程会生成4个vertex数据，生成6个index数据(因为是2个三角形).

MeshPtr NewSimpleRectangleMesh(MeshBuilderFactory* factory) {
  MeshSpec spec{MeshAttribute::kPosition2D | MeshAttribute::kUV};

  // In each vertex, the first two floats represent the position and the second
  // two are UV coordinates.
  vec4 v0(0.f, 0.f, 0.f, 0.f);
  vec4 v1(1.f, 0.f, 1.f, 0.f);
  vec4 v2(1.f, 1.f, 1.f, 1.f);
  vec4 v3(0.f, 1.f, 0.f, 1.f);

  MeshBuilderPtr builder = factory->NewMeshBuilder(spec, 4, 6);
  return builder->AddVertex(v0)
      .AddVertex(v1)
      .AddVertex(v2)
      .AddVertex(v3)
      .AddIndex(0)
      .AddIndex(1)
      .AddIndex(2)
      .AddIndex(0)
      .AddIndex(2)
      .AddIndex(3)
      .Build();
}

前面的mesh过程计算好了一个通用的SimpleRectangle的mesh信息，
具体要显示Rectangle的时候根据具体的显示位置(top_left_position.x/y/z)和显示的大小(size.x/y)来绘制Rectangle.
指定显示的位置可以理解为平移，指定显示的大小可以理解为缩放.
这个平移/缩放过程通过设置transform矩阵来实现，在shader代码中把这个矩阵和通用SimpleRectangle的vertex坐标相乘.

transform矩阵的设置过程如下

Object Object::NewRect(const vec3& top_left_position, const vec2& size,
                       MaterialPtr material) {
  mat4 transform(1);
  transform[0][0] = size.x;
  transform[1][1] = size.y;
  transform[3][0] = top_left_position.x;
  transform[3][1] = top_left_position.y;
  transform[3][2] = top_left_position.z;
  return Object(transform, Shape(Shape::Type::kRect), std::move(material));
}

0x23 Rectangle

下面的代码生成普通Rectangle的Mesh，

下面函数的参数中，
subdivisions指定Rectangle的拆分数，
size指定Rectangle的大小，
top_left指定左上角的坐标，
生成mesh的时候把Rectangle分成(subdivisions*2-1)个小矩形，指定这些小矩形的vertex/index设置.

这个普通Rectangle的mesh和SimpleRectangle的mesh不同之处在于普通Rectangle的mesh是每一个Rectangle生成一个，不具有SimpleRectangle的mesh的通用性. 另外普通Rectangle的mesh会包括更多的小三角形.

MeshPtr NewRectangleMesh(MeshBuilderFactory* factory, const MeshSpec& spec,
                         int subdivisions, vec2 size, vec2 top_left,
                         float top_offset_magnitude,
                         float bottom_offset_magnitude) {
  // Compute the number of vertices in the tessellated circle.
  FXL_DCHECK(subdivisions >= 0);
  size_t vertices_per_side = 2;
  while (subdivisions-- > 0) {
    vertices_per_side *= 2;
  }

  size_t vertex_count = vertices_per_side * 2;
  size_t index_count = (vertices_per_side - 1) * 6;

  auto builder = factory->NewMeshBuilder(spec, vertex_count, index_count);

  // Generate vertex positions.
  constexpr size_t kMaxVertexSize = 100;
  uint8_t vertex[kMaxVertexSize];
  auto vertex_p =
      GetVertexAttributePointers(vertex, kMaxVertexSize, spec, builder);
  FXL_CHECK(vertex_p.pos2);

  const float vertices_per_side_reciprocal = 1.f / (vertices_per_side - 1);
  for (size_t i = 0; i < vertices_per_side; ++i) {
    // Build bottom vertex.
    (*vertex_p.pos2) =
        top_left + vec2(size.x * i * vertices_per_side_reciprocal, size.y);
    if (vertex_p.uv)
      (*vertex_p.uv) = vec2(i * vertices_per_side_reciprocal, 1.f);
    if (vertex_p.pos_offset)
      (*vertex_p.pos_offset) = vec2(0, 1.f * bottom_offset_magnitude);
    if (vertex_p.perim)
      (*vertex_p.perim) = i * vertices_per_side_reciprocal;
    builder->AddVertexData(vertex, builder->vertex_stride());

    // Build top vertex.
    (*vertex_p.pos2) =
        top_left + vec2(size.x * i * vertices_per_side_reciprocal, 0);
    if (vertex_p.uv)
      (*vertex_p.uv) = vec2(i * vertices_per_side_reciprocal, 0);
    if (vertex_p.pos_offset)
      (*vertex_p.pos_offset) = vec2(0, -1.f * top_offset_magnitude);
    if (vertex_p.perim)
      (*vertex_p.perim) = i * vertices_per_side_reciprocal;
    builder->AddVertexData(vertex, builder->vertex_stride());
  }

  // Generate vertex indices.
  for (size_t i = 2; i < vertex_count; i += 2) {
    builder->AddIndex(i - 2);
    builder->AddIndex(i - 1);
    builder->AddIndex(i);
    builder->AddIndex(i);
    builder->AddIndex(i - 1);
    builder->AddIndex(i + 1);
  }

  auto mesh = builder->Build();
  FXL_DCHECK(mesh->num_indices() == index_count);
  return mesh;
}

0x24 Circle

下面分析circle的mesh是如何生成的.

下面函数的参数中，
subdivisions指定Circle的拆分数目，
center指定Circle的中心点坐标.
radius指定Circle的半径大小.

生成mesh的时候是把Circle分成(subdivisions*4)个小扇形，然后计算这些小扇形的vertex/index设置.

MeshPtr NewCircleMesh(MeshBuilderFactory* factory, const MeshSpec& spec,
                      int subdivisions, vec2 center, float radius,
                      float offset_magnitude) {
  // Compute the number of vertices in the tessellated circle.
  FXL_DCHECK(subdivisions >= 0);
  FXL_DCHECK(spec.IsValidOneBufferMesh());
  size_t outer_vertex_count = 4;
  while (subdivisions-- > 0) {
    outer_vertex_count *= 2;
  }

  size_t vertex_count = outer_vertex_count + 1;  // Add 1 for center vertex.
  size_t index_count = outer_vertex_count * 3;

  auto builder = factory->NewMeshBuilder(spec, vertex_count, index_count);

  // Generate vertex positions.
  constexpr size_t kMaxVertexSize = 100;
  uint8_t vertex[kMaxVertexSize];
  auto vertex_p =
      GetVertexAttributePointers(vertex, kMaxVertexSize, spec, builder);

  // Build center vertex.
  FXL_CHECK(vertex_p.pos2);
  (*vertex_p.pos2) = center;
  if (vertex_p.uv)
    (*vertex_p.uv) = vec2(0.5f, 0.5f);
  if (vertex_p.pos_offset)
    (*vertex_p.pos_offset) = vec2(0.f, 0.f);
  // TODO: This is an undesirable singularity.  Perhaps it would be better to
  // treat circles as a ring with inner radius of zero?
  if (vertex_p.perim)
    (*vertex_p.perim) = 0.f;
  builder->AddVertexData(vertex, builder->vertex_stride());

  // Outer vertices.
  const float outer_vertex_count_reciprocal = 1.f / outer_vertex_count;
  const float radian_step = 2 * M_PI / outer_vertex_count;
  for (size_t i = 0; i < outer_vertex_count; ++i) {
    float radians = i * radian_step;

    // Direction of the current vertex from the center of the circle.
    vec2 dir(sin(radians), cos(radians));

    (*vertex_p.pos2) = dir * radius + center;
    if (vertex_p.uv)
      (*vertex_p.uv) = 0.5f * (dir + vec2(1.f, 1.f));
    if (vertex_p.pos_offset)
      (*vertex_p.pos_offset) = dir * offset_magnitude;
    if (vertex_p.perim)
      (*vertex_p.perim) = i * outer_vertex_count_reciprocal;

    builder->AddVertexData(vertex, builder->vertex_stride());
  }

  // Vertex indices.
  for (size_t i = 1; i < outer_vertex_count; ++i) {
    builder->AddIndex(0);
    builder->AddIndex(i + 1);
    builder->AddIndex(i);
  }
  builder->AddIndex(0);
  builder->AddIndex(1);
  builder->AddIndex(outer_vertex_count);

  auto mesh = builder->Build();
  FXL_DCHECK(mesh->num_indices() == index_count);
  FXL_DCHECK(mesh->bounding_box() ==
             BoundingBox(vec3(center.x - radius, center.y - radius, 0),
                         vec3(center.x + radius, center.y + radius, 0)));
  return mesh;
}

前面的mesh过程计算好了一个通用的Circle的mesh信息，
和SimpleRectangle的情况类似，具体绘制Circle的时候根据具体的显示位置(center_position.x/y/z)和显示的大小(radius)来绘制Circle.
指定显示的位置可以理解为平移，指定显示的大小可以理解为缩放.
这个平移/缩放过程也是通过设置transform矩阵来实现，在shader代码中把这个矩阵和通用Circle的vertex坐标相乘.

Object Object::NewCircle(const vec3& center_position, float radius,
                         MaterialPtr material) {
  mat4 transform(1);
  transform[0][0] = radius;
  transform[1][1] = radius;
  transform[3][0] = center_position.x;
  transform[3][1] = center_position.y;
  transform[3][2] = center_position.z;
  return Object(transform, Shape(Shape::Type::kCircle), std::move(material));
}

0x25 RoundRectangle

下面分析生成圆角Rectangle的mesh的代码.

该过程把圆角矩形mesh成三角形，其中的顶点分布如下图所示,

其中每个圆角部分被拆分成8个小扇形.

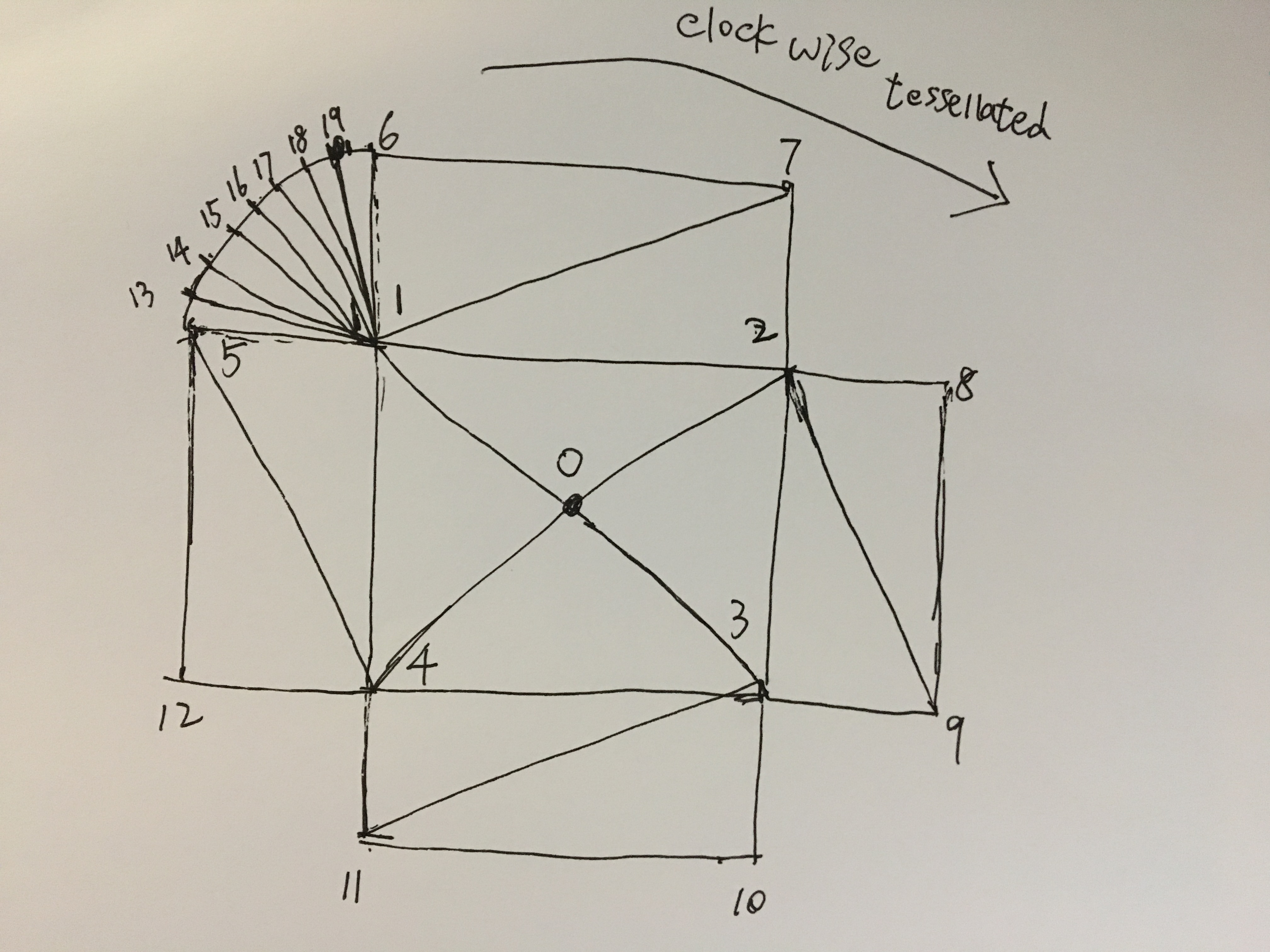
0 ~ 12 顶点是中间部分的矩形对应的顶点.
13 ~ 19 顶点是左上角部分的圆角对应的顶点.
20 ~ 26 顶点是右上角部分的圆角对应的顶点.
27 ~ 33 顶点是右下角部分的圆角对应的顶点.
34 ~ 40 顶点是左下角部分的圆角对应的顶点.

NewRoundedRect是总的入口函数，其中会调用GenerateRoundedRectIndices()来根据顶点来构造三角形，调用GenerateRoundedRectVertexUVs()生成纹理坐标，最后调用GenerateRoundedRectVertexPositionsFromUVs()来生成顶点坐标.

MeshPtr RoundedRectFactory::NewRoundedRect(
    const RoundedRectSpec& spec, const MeshSpec& mesh_spec,
    BatchGpuUploader* batch_gpu_uploader) {
  FXL_DCHECK(batch_gpu_uploader);

  auto index_buffer = GetIndexBuffer(spec, mesh_spec, batch_gpu_uploader);

  auto counts = GetRoundedRectMeshVertexAndIndexCounts(spec);
  const uint32_t vertex_count = counts.first;
  const uint32_t index_count = counts.second;
  const size_t primary_buffer_stride = mesh_spec.stride(0);
  const size_t secondary_buffer_stride = mesh_spec.stride(1);

  const size_t vertex_buffer_size =
      vertex_count * (primary_buffer_stride + secondary_buffer_stride);

  auto vertex_buffer =
      buffer_factory_.NewBuffer(vertex_buffer_size,
                                vk::BufferUsageFlagBits::eVertexBuffer |
                                    vk::BufferUsageFlagBits::eTransferDst,
                                vk::MemoryPropertyFlagBits::eDeviceLocal);

  const auto bounding_box =
      BoundingBox::NewChecked(-0.5f * vec3(spec.width, spec.height, 0),
                              0.5f * vec3(spec.width, spec.height, 0), 1);

  switch (mesh_spec.vertex_buffer_count()) {
    case 1: {
      auto writer = batch_gpu_uploader->AcquireWriter(vertex_buffer_size);
      GenerateRoundedRectVertices(spec, mesh_spec, writer->host_ptr(),
                                  writer->size());
      writer->WriteBuffer(vertex_buffer, {0, 0, vertex_buffer->size()});
      batch_gpu_uploader->PostWriter(std::move(writer));

      return fxl::MakeRefCounted<Mesh>(
          static_cast<ResourceRecycler*>(this), mesh_spec, bounding_box,
          vertex_count, index_count, vertex_buffer, std::move(index_buffer));
    }
    case 2: {
      auto writer = batch_gpu_uploader->AcquireWriter(vertex_buffer_size);
      GenerateRoundedRectVertices(
          spec, mesh_spec, writer->host_ptr(),
          vertex_count * primary_buffer_stride,
          writer->host_ptr() + vertex_count * primary_buffer_stride,
          vertex_count * secondary_buffer_stride);
      writer->WriteBuffer(vertex_buffer, {0, 0, vertex_buffer->size()});
      batch_gpu_uploader->PostWriter(std::move(writer));

      return fxl::MakeRefCounted<Mesh>(
          static_cast<ResourceRecycler*>(this), mesh_spec, bounding_box,
          index_count, std::move(index_buffer), 0, vertex_count, vertex_buffer,
          0, std::move(vertex_buffer), vertex_count * primary_buffer_stride);
    }
    default:
      FXL_CHECK(false) << "unsupported vertex buffer count: "
                       << mesh_spec.vertex_buffer_count();
      return nullptr;
  }
}

下面的代码是构造圆角Rectangle中的三角形的过程，indices中保存的是把这些顶点拼接成三角形的顶点索引.

void GenerateRoundedRectIndices(const RoundedRectSpec& spec,
                                const MeshSpec& mesh_spec, void* indices_out,
                                uint32_t max_bytes) {
  TRACE_DURATION("gfx", "escher::GenerateRoundedRectIndices");

  FXL_DCHECK(max_bytes >= kIndexCount * sizeof(uint32_t));
  uint32_t* indices = static_cast<uint32_t*>(indices_out);

  // Central square triangles.
  indices[0] = 0;
  indices[1] = 4;
  indices[2] = 1;
  indices[3] = 0;
  indices[4] = 1;
  indices[5] = 2;
  indices[6] = 0;
  indices[7] = 2;
  indices[8] = 3;
  indices[9] = 0;
  indices[10] = 3;
  indices[11] = 4;

  // "Cross arm 1"  triangles.
  indices[12] = 1;
  indices[13] = 7;
  indices[14] = 2;
  indices[15] = 1;
  indices[16] = 6;
  indices[17] = 7;

  // "Cross arm 2"  triangles.
  indices[18] = 2;
  indices[19] = 9;
  indices[20] = 3;
  indices[21] = 2;
  indices[22] = 8;
  indices[23] = 9;

  // "Cross arm 3"  triangles.
  indices[24] = 3;
  indices[25] = 11;
  indices[26] = 4;
  indices[27] = 3;
  indices[28] = 10;
  indices[29] = 11;

  // "Cross arm 4"  triangles.
  indices[30] = 4;
  indices[31] = 5;
  indices[32] = 1;
  indices[33] = 4;
  indices[34] = 12;
  indices[35] = 5;

  // WARNING: here's where it gets confusing; the number of indices generated is
  // dependent on kCornerDivisions.

  // We've already generated output indices for the "cross triangles".
  constexpr uint32_t kCrossTriangles = 12;
  // Holds the position of the next index to output.
  uint32_t out = kCrossTriangles * 3;
  // Holds the highest index of any vertex used thus far (the central "cross"
  // consists of 13 vertices, whose indices are 0-12).
  uint32_t highest_index = 12;

  // These are the indices of the 4 triangles that would be output if
  // kCornerDivisions were zero.
  const uint32_t corner_tris[] = {1, 6, 5, 2, 8, 7, 3, 10, 9, 4, 12, 11};

  // For each corner, generate wedges in clockwise order.
  for (uint32_t corner = 0; corner < 4; ++corner) {
    // Index of the vertex at the center of the current corner.
    const uint32_t center = corner_tris[corner * 3];
    // As we move clockwise around the corner, this holds the index of the
    // previous perimeter vertex.
    uint32_t prev = corner_tris[corner * 3 + 2];

    for (uint32_t i = 0; i < kCornerDivisions; ++i) {
      indices[out++] = center;
      indices[out++] = prev;
      indices[out++] = prev = ++highest_index;
    }
    // One last triangle (or the only one, if kCornerDivisions == 0).
    indices[out++] = center;
    indices[out++] = prev;
    indices[out++] = corner_tris[corner * 3 + 1];
  }

  FXL_DCHECK(out == kIndexCount);
}

下面函数计算这些点(0 ~ 40)对应的纹理(uv)坐标.

template <typename VertT>
void GenerateRoundedRectVertexUVs(const RoundedRectSpec& spec, VertT* verts) {
  TRACE_DURATION("gfx", "escher::GenerateRoundedRectVertexUVs");

  const float width = spec.width;
  const float height = spec.height;

  // First compute UV coordinates of the four "corner centers".
  verts[1].uv =
      vec2(spec.top_left_radius / width, spec.top_left_radius / height);
  verts[2].uv =
      vec2(1.f - spec.top_right_radius / width, spec.top_right_radius / height);
  verts[3].uv = vec2(1.f - spec.bottom_right_radius / width,
                     1.f - spec.bottom_right_radius / height);
  verts[4].uv = vec2(spec.bottom_left_radius / width,
                     1.f - spec.bottom_left_radius / height);

  // The "center" vertex is the average of the four "corner centers".
  verts[0].uv =
      0.25f * ((verts[1].uv + verts[2].uv + verts[3].uv + verts[4].uv));

  // Next, compute UV coords for the 8 vertices where the rounded corners meet
  // the straight side sections.
  verts[6].uv = vec2(verts[1].uv.x, 0.f);
  verts[7].uv = vec2(verts[2].uv.x, 0.f);
  verts[8].uv = vec2(1.f, verts[2].uv.y);
  verts[9].uv = vec2(1.f, verts[3].uv.y);
  verts[10].uv = vec2(verts[3].uv.x, 1.f);
  verts[11].uv = vec2(verts[4].uv.x, 1.f);
  verts[12].uv = vec2(0.f, verts[4].uv.y);
  verts[5].uv = vec2(0.f, verts[1].uv.y);

  // Next, compute UV coords for the vertices that make up the rounded corners.
  // We start at index 13; indices 0-12 were computed above.
  uint32_t out = 13;

  constexpr float kPI = 3.14159265f;
  constexpr float kAngleStep = kPI / 2 / (kCornerDivisions + 1);

  // Generate UV coordinates for top-left corner.
  float angle = kPI + kAngleStep;
  vec2 scale =
      vec2(spec.top_left_radius / width, spec.top_left_radius / height);
  for (size_t i = 0; i < kCornerDivisions; ++i) {
    verts[out++].uv = verts[1].uv + vec2(cos(angle), sin(angle)) * scale;
    angle += kAngleStep;
  }

  // Generate UV coordinates for top-right corner.
  angle = 1.5f * kPI + kAngleStep;
  scale = vec2(spec.top_right_radius / width, spec.top_right_radius / height);
  for (size_t i = 0; i < kCornerDivisions; ++i) {
    verts[out++].uv = verts[2].uv + vec2(cos(angle), sin(angle)) * scale;
    angle += kAngleStep;
  }

  // Generate UV coordinates for bottom-right corner.
  angle = kAngleStep;
  scale =
      vec2(spec.bottom_right_radius / width, spec.bottom_right_radius / height);
  for (size_t i = 0; i < kCornerDivisions; ++i) {
    verts[out++].uv = verts[3].uv + vec2(cos(angle), sin(angle)) * scale;
    angle += kAngleStep;
  }

  // Generate UV coordinates for bottom-right corner.
  angle = 0.5f * kPI + kAngleStep;
  scale =
      vec2(spec.bottom_left_radius / width, spec.bottom_left_radius / height);
  for (size_t i = 0; i < kCornerDivisions; ++i) {
    verts[out++].uv = verts[4].uv + vec2(cos(angle), sin(angle)) * scale;
    angle += kAngleStep;
  }
}

下面函数计算这些点(0 ~ 40)对应的顶点坐标，根据对应的纹理坐标来计算得到.

// Helper for GenerateRoundedRectVertices().
template <typename UvVertT, typename PosVertT>
void GenerateRoundedRectVertexPositionsFromUVs(const RoundedRectSpec& spec,
                                               UvVertT* uv_verts,
                                               PosVertT* pos_verts) {
  TRACE_DURATION("gfx", "escher::GenerateRoundedRectVertexPositionsFromUVs");

  const vec2 extent(spec.width, spec.height);
  const vec2 offset = -0.5f * extent;
  for (size_t i = 0; i < kVertexCount; ++i) {
    pos_verts[i].pos = uv_verts[i].uv * extent + offset;
  }
}

0x26 Sphere

下面是构造Sphere的mesh的代码.

MeshPtr NewSphereMesh(MeshBuilderFactory* factory, const MeshSpec& spec,
                      int subdivisions, vec3 center, float radius) {
  FXL_DCHECK(subdivisions >= 0);
  FXL_DCHECK(spec.IsValidOneBufferMesh());
  size_t vertex_count = 9;
  size_t triangle_count = 8;
  for (int i = 0; i < subdivisions; ++i) {
    // At each level of subdivision, an additional vertex is added for each
    // triangle, and each triangle is split into three.
    vertex_count += triangle_count;
    triangle_count *= 3;
  }

  // Populate initial octahedron.
  auto builder =
      factory->NewMeshBuilder(spec, vertex_count, triangle_count * 3);
  constexpr size_t kMaxVertexSize = 100;
  uint8_t vertex[kMaxVertexSize];
  auto vertex_p =
      GetVertexAttributePointers(vertex, kMaxVertexSize, spec, builder);
  FXL_CHECK(vertex_p.pos3);

  // Positions and UV-coordinates for the initial octahedron.  The vertex with
  // position (-radius, 0, 0) is replicated 4 times, with different UV-coords
  // each time.  This is a consequence of surface parameterization that is
  // described in the header file.
  const vec3 positions[] = {vec3(radius, 0.f, 0.f),  vec3(0.f, 0.f, radius),
                            vec3(0.f, -radius, 0.f), vec3(0.f, 0.f, -radius),
                            vec3(0.f, radius, 0.f),  vec3(-radius, 0.f, 0.f),
                            vec3(-radius, 0.f, 0.f), vec3(-radius, 0.f, 0.f),
                            vec3(-radius, 0.f, 0.f)};
  const vec2 uv_coords[] = {vec2(.5f, .5f), vec2(1.f, .5f), vec2(.5f, 0.f),
                            vec2(0.f, .5f), vec2(.5f, 1.f), vec2(0.f, 0.f),
                            vec2(1.f, 0.f), vec2(1.f, 1.f), vec2(0.f, 1.f)};

  for (int i = 0; i < 9; ++i) {
    (*vertex_p.pos3) = positions[i] + center;
    if (vertex_p.uv) {
      (*vertex_p.uv) = uv_coords[i];
    }
    builder->AddVertexData(vertex, builder->vertex_stride());
  }
  builder->AddTriangle(0, 1, 2)
      .AddTriangle(0, 2, 3)
      .AddTriangle(0, 3, 4)
      .AddTriangle(0, 4, 1)
      .AddTriangle(5, 2, 1)
      .AddTriangle(6, 3, 2)
      .AddTriangle(7, 4, 3)
      .AddTriangle(8, 1, 4);

  // TODO(ES-32): this is a hack to ease implementation.  We don't currently
  // need any tessellated spheres; this is just a way to verify that 3D meshes
  // are working properly.
  FXL_DCHECK(spec.attributes[0] ==
             (MeshAttribute::kPosition3D | MeshAttribute::kUV))
      << "Tessellated sphere must have UV-coordinates.";
  size_t position_offset = reinterpret_cast<uint8_t*>(vertex_p.pos3) - vertex;
  size_t uv_offset = reinterpret_cast<uint8_t*>(vertex_p.uv) - vertex;
  while (subdivisions-- > 0) {
    // For each level of subdivision, iterate over all existing triangles and
    // split them into three.
    // TODO(ES-32): see comment in header file... this approach is broken, but
    // sufficient for our current purpose.
    const size_t subdiv_triangle_count = builder->index_count() / 3;
    FXL_DCHECK(subdiv_triangle_count * 3 == builder->index_count());

    for (size_t tri_ind = 0; tri_ind < subdiv_triangle_count; ++tri_ind) {
      // Obtain indices for the current triangle, and the position/UV coords for
      // the corresponding vertices.
      uint32_t* tri = builder->GetIndex(tri_ind * 3);
      uint32_t ind0 = tri[0];
      uint32_t ind1 = tri[1];
      uint32_t ind2 = tri[2];
      uint8_t* vert0 = builder->GetVertex(ind0);
      uint8_t* vert1 = builder->GetVertex(ind1);
      uint8_t* vert2 = builder->GetVertex(ind2);
      vec3 pos0 = *reinterpret_cast<vec3*>(vert0 + position_offset);
      vec3 pos1 = *reinterpret_cast<vec3*>(vert1 + position_offset);
      vec3 pos2 = *reinterpret_cast<vec3*>(vert2 + position_offset);
      vec2 uv0 = *reinterpret_cast<vec2*>(vert0 + uv_offset);
      vec2 uv1 = *reinterpret_cast<vec2*>(vert1 + uv_offset);
      vec2 uv2 = *reinterpret_cast<vec2*>(vert2 + uv_offset);

      // Create a new vertex by averaging the existing vertex attributes.
      (*vertex_p.pos3) =
          center + radius * glm::normalize((pos0 + pos1 + pos2) / 3.f - center);
      (*vertex_p.uv) = (uv0 + uv1 + uv2) / 3.f;
      builder->AddVertexData(vertex, builder->vertex_stride());

      // Replace the current triangle in-place with a new triangle that refers
      // to the new vertex.  Then, add two new triangles that also refer to the
      // new vertex.
      uint32_t new_ind = builder->vertex_count() - 1;
      tri[2] = new_ind;
      builder->AddTriangle(ind1, ind2, new_ind)
          .AddTriangle(ind2, ind0, new_ind);
    }
  }
  return builder->Build();
}

0x27 Ring

下面分析Ring的mesh是如何生成的, Ring是由内圈和外圈包含的区域组成, 内圈区域内是透明的, 实际上Ring的mesh没有包括内圈，也就是说渲染的时候不会去绘制内圈区域, 所以mesh生成的绘制区域只需要包括内圈和外圈组成的区域，mesh的过程也就是把内圈和外圈之间的区域拆分成许多小三角形.

下面函数的参数中，
subdivisions指定Ring的拆分数.
center指定Circle的中心点坐标.
outer_radius指定Ring的外圈半径.
inner_radius指定Ring的内圈半径.

生成mesh的时候把Ring分成(subdivisions*4)个小扇形，这些小扇形会和Ring的内圈和外圈相交,
指定相交点的vertex值，然后把这些vertex组成的triangle，vertex的index值指定给mesh的index.

MeshPtr NewRingMesh(MeshBuilderFactory* factory, const MeshSpec& spec,
                    int subdivisions, vec2 center, float outer_radius,
                    float inner_radius, float outer_offset_magnitude,
                    float inner_offset_magnitude) {
  // Compute the number of vertices in the tessellated circle.
  FXL_DCHECK(subdivisions >= 0);
  FXL_DCHECK(spec.IsValidOneBufferMesh());
  size_t outer_vertex_count = 4;
  while (subdivisions-- > 0) {
    outer_vertex_count *= 2;
  }

  size_t vertex_count = outer_vertex_count * 2;
  size_t index_count = outer_vertex_count * 6;

  auto builder = factory->NewMeshBuilder(spec, vertex_count, index_count);

  // Generate vertex positions.
  constexpr size_t kMaxVertexSize = 100;
  uint8_t vertex[kMaxVertexSize];
  auto vertex_p =
      GetVertexAttributePointers(vertex, kMaxVertexSize, spec, builder);
  FXL_CHECK(vertex_p.pos2);

  const float outer_vertex_count_reciprocal = 1.f / outer_vertex_count;
  const float radian_step = 2 * M_PI / outer_vertex_count;
  for (size_t i = 0; i < outer_vertex_count; ++i) {
    float radians = i * radian_step;

    // Direction of the current vertex from the center of the circle.
    vec2 dir(sin(radians), cos(radians));

    // Build outer-ring vertex.
    (*vertex_p.pos2) = dir * outer_radius + center;
    if (vertex_p.uv) {
      // Munge the texcoords slightly to avoid wrapping artifacts.  This matters
      // when both:
      //   - the vk::SamplerAddressMode is eRepeat
      //   - the vk::Filter is eLinear
      (*vertex_p.uv) = 0.49f * (dir + vec2(1.f, 1.02f));
      // TODO(ES-108): once we can specify a SamplerAddressMode of eClampToEdge,
      // remove the hack above and replace it with the code below:
      // (*vertex_p.uv) = 0.5f * (dir + vec2(1.f, 1.f));
    }
    if (vertex_p.pos_offset)
      (*vertex_p.pos_offset) = dir * outer_offset_magnitude;
    if (vertex_p.perim)
      (*vertex_p.perim) = i * outer_vertex_count_reciprocal;
    builder->AddVertexData(vertex, builder->vertex_stride());

    // Build inner-ring vertex.  Only the position and offset may differ from
    // the corresponding outer-ring vertex.
    (*vertex_p.pos2) = dir * inner_radius + center;
    if (vertex_p.pos_offset) {
      // Positive offsets point inward, toward the center of the circle.
      (*vertex_p.pos_offset) = dir * -inner_offset_magnitude;
    }
    builder->AddVertexData(vertex, builder->vertex_stride());
  }

  // Generate vertex indices.
  for (size_t i = 2; i < vertex_count; i += 2) {
    builder->AddIndex(i - 2);
    builder->AddIndex(i - 1);
    builder->AddIndex(i);
    builder->AddIndex(i);
    builder->AddIndex(i - 1);
    builder->AddIndex(i + 1);
  }
  builder->AddIndex(vertex_count - 2);
  builder->AddIndex(vertex_count - 1);
  builder->AddIndex(0);
  builder->AddIndex(0);
  builder->AddIndex(vertex_count - 1);
  builder->AddIndex(1);

  auto mesh = builder->Build();
  FXL_DCHECK(mesh->num_indices() == index_count);
  FXL_DCHECK(
      mesh->bounding_box() ==
      BoundingBox(vec3(center.x - outer_radius, center.y - outer_radius, 0),
                  vec3(center.x + outer_radius, center.y + outer_radius, 0)));
  return mesh;
}